[칼럼] 나의 물리1 비역학 문풀법
안녕하세요! 이번에는 물리1에서 대표적으로 출제되는 준킬러 또는 킬러 문제에 대한 저의 접근법과 풀이법에 관해서 써보겠습니다...!! 물리1 전문가 분들이 많이 계신 만큼, 이미 널리 알려진 스킬들과 꽤 겹치겠지만요... *작성하다 보니 너무 길어질 것 같아서, 역학 파트는 다음 글에서 따로 다루겠습니다ㅜㅜ
아무래도 문제를 예시로 사용해야 할 상황이 있을텐데, 제가 n제나 실모를 전부 폐기 처분해서 2022학년도 수능 문제들만 예시로 활용할게요. 그럼 시작합니다! (난이도 표기는 저의 주관적 의견입니다.)
1. 개념 학습
일반적으로 노베 상태에서 물리1을 처음 공부하는 상황이라면, 유명한 강사 분들의 인강을 듣는게 좋다고 생각합니다. 물리1은 자잘한 지엽 개념들이 은근히 있어 개념의 중요성을 판단하기 어렵고, 특수 상대성 이론이나 전자기 유도 등의 개념처럼 스스로 이해하기 쉽지 않은 내용도 포함되어 있습니다. 그렇기 때문에 검증된 강사 분들의 설명이 베이스가 부족한 학생들의 개념 학습 효율을 크게 상승시킬 것이라고 예상합니다. (참고로 저는 인강 안 들어봐서 강사 추천은 불가능합니다.)
2. 열역학 파트 (난이도: 4/10)
○ 대표적인 준킬러 출제 내용: 열기관의 P-V, P-T, V-T 그래프 해석, 이상 기체의 열역학 과정 해석
2022 수능에서는 열기관의 V-T 그래프 해석 관련 문제가 준킬러로 출제되었습니다. 기존 평가원 기출에서는 주로 P-V 그래프를 다룬 반면, 수험생들에게 상대적으로 생소한 V-T 그래프가 출제되어 체감 난이도가 높았을 것으로 예상됩니다. 이상 기체의 열역학 과정이 따르는 경로의 밑면적이 기체가 한 일이 된다는 점에서 P-V 그래프가 자주 사용되고 쉬운 건 사실이지만, 이상 기체 상태 방정식 (PV=nRT)과 여러 가지 열역학 과정을 잘 알고 있다면 어떤 두 가지 변수가 주어지더라도 그래프를 해석하는 게 그닥 어려운 일은 아니라고 생각합니다. 그리고 이렇게 V-T 그래프가 수능 문제로 출제된 만큼, 앞으로의 수능을 준비할 때 V-T나 P-T 그래프가 포함된 사설 문제들도 거르지 말아야겠죠? 그럼 많은 수험생들을 당황케 한 2022 수능의 17번 문제를 한번 풀어봅시다.
어떤 두 가지 변수가 주어지든 간에, 열기관의 그래프를 해석하기 위해 가장 먼저 해야 할 일은 열역학 과정의 순환을 이루는 각 점의 상태 (P, V, T)를 파악하는 것입니다. 이것만 파악해도 문제 절반 넘게 푸셨다고 봐도 됩니다. 이를 각 점에 알아볼 수 있게 표시한 다음, 직선 또는 곡선으로 표현되는 점 사이의 경로에 그 경로가 어떤 열역학 과정에 해당하는지를 적습니다. 아래 문제에서는 A->B가 등압 과정임이 주어져 있고, B->C는 부피가 일정하니 등적 과정, C->A는 온도가 일정하니 등온 과정이겠네요. 그리고 각각의 과정이 지니는 특성을 생각하며 선지의 정오를 판단하면 되는데, ㄱ은 절대온도가 증가하는 과정이고 이상 기체의 내부 에너지는 절대온도에 비례하므로 옳은 선지입니다. ㄴ과 ㄷ은 각각 열효율과 기체가 한 번 순환하는 동안 한 일을 직접 계산해보면 되는데, "W(열기관이 한 일)=Qh(순환 과정 동안 흡수한 열) - Qc(순환 과정 동안 방출한 열)"임을 기억하고 있으면 아래의 풀이처럼 구할 수 있습니다. 여기서 W_등온은 빨간색으로 색칠한 면적인데 점 A와 C, 그리고 A와 C를 P축에 내린 수선의 발 2개를 꼭짓점으로 하는 사다리꼴보다 면적이 작으므로 가장 아래에 있는 부등식이 성립하는 건 아시죠?
정리하면, 열역학 파트에서는 기체의 열역학 과정 4가지 유형 (등온 과정, 등압 과정, 등적 과정, 단열 과정)의 특성을 열역학 제1법칙과 관련지어 확실히 기억하고, PV=nRT의 이상 기체 상태 방정식을 알고 있으면 대부분의 준킬러 문제들을 풀이할 수 있습니다. 비킬러 출제 가능성도 있으니, 언급한 내용 외의 열역학 제2법칙이나 열효율 등의 개념에 대해서도 당연히 암기하고 있어야 하고요.


2022학년도 수능 물리학1 17번 문항
3. 특수 상대성 이론 파트 (난이도: 8/10)
○ 대표적인 킬러/준킬러 출제 내용: 사건의 측정과 동시성의 상대성, 시간 지연과 길이 수축
2022 수능에서는 핵반응식 관련 비킬러 문제 하나와 시간 지연과 길이 수축 관련 준킬러/킬러 문제 하나가 출제되었습니다. 여기서 준킬러/킬러라고 표현한 것은 시간 지연을 얼마나 잘 이해했느냐에 따라 문제의 난이도가 크게 달라지기 때문입니다. 한 번 머리가 '띵'하면서 이해하고 나면 문제의 유형에 관계 없이 수월하게 접근할 수 있다는 점에서 역학 파트와 닮은 것 같네요. 해당 내용을 제대로 이해하기 위해서는 인강 강사 분들의 설명을 듣는 것도 좋지만, 결국 여러 유형의 문제를 풀면서 자신의 생각이 지닌 오류를 바로잡아 나가는 과정이 큰 도움이 된다고 생각합니다. 저도 부끄럽지만 세 번째 수능을 준비하면서 강민웅T의 특난도 특강을 다 풀어갈 때가 돼서야 제대로 이해했다는 생각이 들더라구요... 각설하고, 관련 문제인 2022 수능의 14번 풀어보겠습니다!
이 문제는 예년도에 출제되었던 동시성의 상대성 관련 문제에 비해서는 다소 쉬운 편이라고 생각합니다. 다만 정신 없는 타임 어택으로 인해 체감 난이도는 조금 높았을 수 있겠네요. 우선 A의 관성계에서 우주선은 +x방향으로 등속도 운동하고 있는데 광원->p와 광원->q가 걸린 시간이 같고, p가 광원의 초기 위치에 가까워지고 있고 q는 멀어지고 있다는 점을 고려하면, 길이를 비교했을 때 광원->p가 광원->q보다 긺을 알 수 있습니다. 그리고 광원과 함께 운동하는 B의 관성계에서 광원->q와 광원->r이 걸린 시간이 같으므로, 광원->q와 광원->r의 길이가 같음을 알 수 있겠네요. 정리하면, [광원->p] > [광원->q] = [광원->r]가 됩니다. 이제 선지를 보며 정오를 판단하면 되는데, ㄱ은 빛과 p의 상대 운동을 고려하면 틀린 선지이고, ㄴ은 A의 입장에서 광원->r에 걸린 시간이 시간 지연이 일어난 상황이고 B의 입장에서 광원->r에 걸린 시간이 고유 시간임을 고려하면 맞는 선지입니다. 마지막으로 ㄷ은 앞에서 구한 빛의 경로 길이 간의 부등식에 의해 맞는 선지구요.
결국 동시성의 상대성 또는 시간 지연과 관련된 문제를 풀 때 핵심 포인트는 어떤 관찰자의 입장에서 일어나는 사건 간의 간격이 고유 시간이 되는지를 파악하는 것이라고 생각합니다. 그럼 나머지 관찰자의 입장에서 일어난 같은 사건 간의 간격은 모두 시간 지연이 적용된 상황이 되겠죠. 이것을 주어진 문제 상황에 따라 그때그때 제대로 파악하기 위해서는 위에서 밑줄 그은 과정을 열심히 하시면 됩니다.

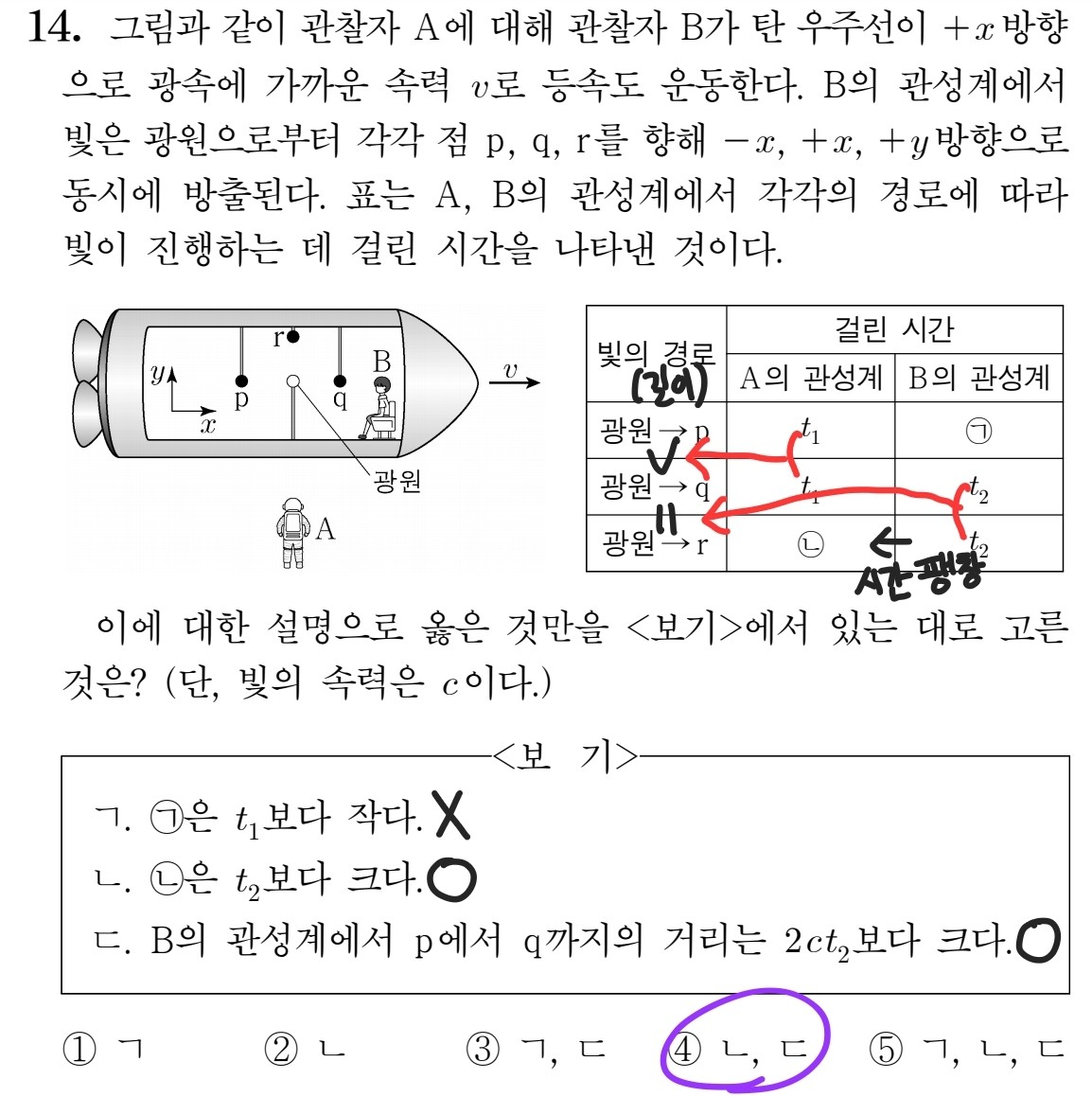
2022학년도 수능 물리학1 14번 문항
4. 전기장 파트 (난이도: 6/10)
○ 대표적인 준킬러 출제 내용: p-n 접합 다이오드의 특성 응용 (살짝 퍼즐)
2022 수능에서는 보어의 수소 원자 모형, p-n 접합 다이오드의 특성, 일직선 상에 위치한 점전하 4개(!)에 의해 양전하가 받는 전기력 관련 문제가 각각 1개씩 출제되었습니다. 보어의 수소 원자 모형 문제는 개념 학습으로 충분히 풀 수 있으니 따로 언급하지 않겠습니다. p-n 접합 다이오드의 특성 관련 문제들도 사실 어렵지 않은 편에 속하지만, 복잡한 퍼즐화가 충분히 가능하다는 점과 대체로 시험지의 중반부에 3점 문항으로 출제된다는 점을 고려하여 준킬러로 취급했습니다. 그럼 2022 수능에서 관련 문제로 출제된 10번을 한번 보겠습니다.
실험 결과로 제시된 표를 보고 번호를 매긴 다이오드의 방향을 파악하는 것이 핵심입니다. (나)의 결과만으로는 알 수 있는 게 많지 않으니, (다)의 결과와 함께 봅시다. (다)에서 스위치 S_1만 닫았는데, c->S_1->d의 방향으로 전류가 흘렀고 a 또는 b가 전류 흐름의 시점과 종점이 되어야 하기 때문에, 가능한 경우는 b->3번 다이오드->c->S_1->d->2번 다이오드->a 가 유일함을 알 수 있습니다. 그렇기 때문에 아래의 노란 상자 윗줄과 같은 결론이 도출됩니다. 그리고 (나)에서 전류가 흐르지 않았기 때문에, 1번 다이오드의 방향도 노란 상자 아랫줄의 그림으로 결정됩니다. 이를 통해 ㄱ과 ㄴ 선지의 정오를 판단할 수 있고, ㄷ 선지는 주어진 그림에서 a와 b를 바꾸고 S_1과 S_2를 모두 닫았을 때의 상황을 그려서 정오를 판단할 수 있습니다.
이 문제의 경우에는 비교적 간단하게 풀렸지만, 다이오드의 숫자 증가 또는 실험 결과의 빈 칸 증가 등을 통해 마음만 먹으면 어려운 퍼즐 형식의 문제를 만들 수 있다는 점에서 앞으로의 출제가 기대(?)되는 유형입니다. 문제가 더 복잡해지더라도 다이오드가 포함된 회로에서 전류가 흐르기 위해서는 회로에 포함된 모든 다이오드가 순방향인 닫힌 회로가 존재해야 한다는 점을 바탕으로, 여러 가지 케이스 중에서 가능한 케이스를 논리적으로 도출하면 충분히 풀이할 수 있을 것입니다.

2022학년도 수능 물리학1 10번 문항
○ 대표적인 킬러 출제 내용: 일직선 상에 위치한 점전하 n개 사이에 작용하는 전기력 해석 (퍼즐)
아마 작년에 수능 물리1을 응시하신 수험생 분들이 비주얼적으로 가장 충격을 받았을 법한 문제라고 생각합니다. 점전하가 5개나 있다!? 하지만 2점 문제인 만큼 막상 문제를 풀어보면 비주얼에 비해서 허무한 난이도를 갖고 있음을 알 수 있습니다. 기존에 퍼즐 유형으로 출제되었던 비슷한 문제들과 비교해서 퍼즐을 풀 필요가 딱히 없어서 어렵지 않은 문제입니다. 2022 수능에서 관련 문제로 출제된 19번 문항 같이 보겠습니다.
우선 발문에서 빨간 밑줄로 표시한 부분에서 상당히 많은 정보를 제공합니다. 이 정보를 기호로 (가)의 그림 위에 표시하여 다시 발문을 읽을 필요가 없도록 하는 것이 가장 먼저 해야 할 일입니다. 그리고 (가)의 그림에서 3d<x<5d인 구간에서는 P에 작용하는 전기력이 -x방향임을 알 수 있으므로, (나)의 그래프와 비교하여 x축의 윗부분이 +x방향임을 확인할 수 있습니다. 이를 바탕으로 (나)의 그래프를 보면 ㄱ 선지는 참입니다. (나)의 그래프에서 x=2d일 때 P에 작용하는 전기력이 0임을 활용하여 식을 세우면, 노란 상자와 같은 결론을 얻을 수 있습니다. 따라서 ㄴ 선지 역시 참입니다. 이제 ㄷ 선지에서 언급한 5d<x<6d의 구간만 확인하면 됩니다. 수학적인 직관이 뛰어나신 분들은 대칭성에 근거하여 바로 ㄷ 선지가 거짓임을 파악하실 수 있겠지만, 저처럼 그렇지 못한 분들은 아래에 노란색으로 괄호 친 부분과 같이 양 끝점에서 작용하는 전기력을 확인한 후, P가 5d에서 6d의 위치로 향할수록 P에 작용하는 전기력이 감소한다는 사실을 파악하여 ㄷ 선지를 거짓으로 결론 내리시면 됩니다.

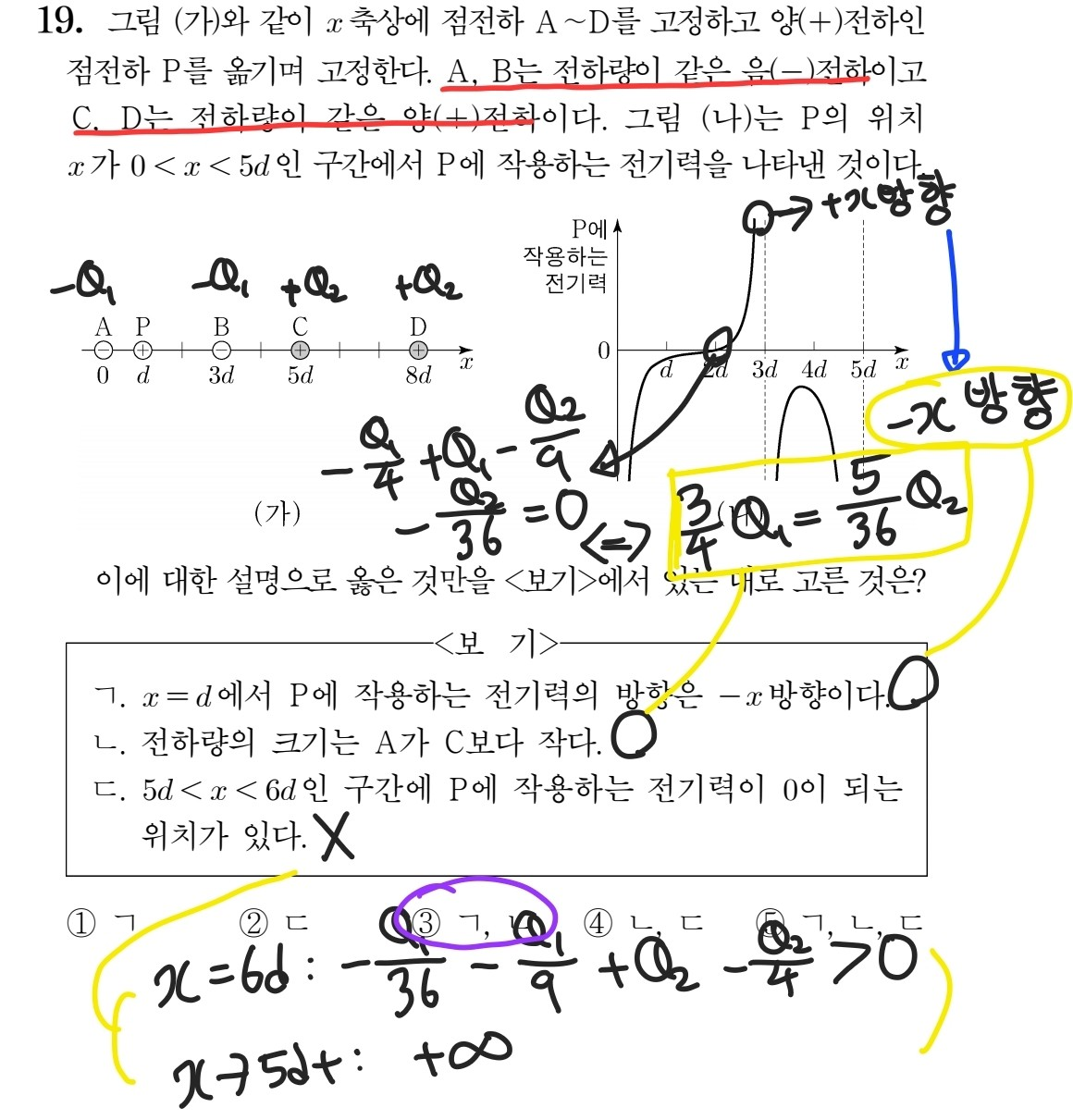
2022학년도 수능 물리학1 19번 문항
위에서 말씀드린 것처럼 막상 풀어보니 기존에 보던 점전하 문제에 비해 쉽지 않나요? 하지만 실모에서 자주 출제되는 형태의 점전하 퍼즐 문제가 언제 또 수능에 나올지 모르니, 대비는 해두어야겠죠? 그런 의미에서 퍼즐의 느낌이 강하지는 않지만, 지금까지 평가원에서 출제되었던 해당 유형의 문제 중에 가장 까다롭다고 생각되는 2021학년도 9월 모의고사 19번 문항을 한번 풀어보겠습니다.
문제의 풀이는 1)부터 4)까지 따라 보시면 충분히 이해하실 수 있을 것 같네요. 이 문제에서 퍼즐의 요소가 포함되어 있는 부분은 1)과 2) 정도가 끝인데, 그 요소들이 좀 더 복잡한 점전하 퍼즐 문제를 풀이할 때도 핵심이 되기 때문에 확실히 짚고 넘어갈 필요가 있습니다. 우선 이 문제처럼 점전하의 배치가 여러 가지로 주어진 경우에는, (가)와 (나)처럼 하나의 점전하만 위치가 바뀐 형태의 배치 쌍이 존재하는지 확인합니다. 만약 존재한다면, 그 배치 쌍의 비교를 통해 논리적으로 위치가 바뀐 점전하의 부호 또는 세기를 파악할 수 있을 것입니다. 그리고 n개의 점전하가 있는데 (n-1)개의 점전하의 부호를 알고 있고, 그 중 하나의 점전하가 받는 힘의 방향을 알고 있다면 2)와 같이 나머지 하나의 점전하의 부호도 논리적으로 도출될 가능성이 높습니다.
이후에 이 문제처럼 쿨롱 법칙을 통해 연립방정식을 세워야 하는 상황이면, 어차피 저희가 문제에서 알고자 하는 것은 대부분 점전하의 부호와 상대적인 세기이기 때문에, 쿨롱 상수 k와 거리의 단위가 되는 문자 (여기서는 d)를 모두 1로 취급하는 것이 훨씬 간편합니다. 연립일차방정식은 본인이 편한 순서대로 연립하여 풀면 되겠죠?
이보다 더 고난도인 점전하 퍼즐 문제에서는 A와 B가 각각 (+,+), (+,-), (-,+), (-,-) 중 어떤 부호의 조합을 갖는지 네 가지 조합에 따른 결과를 비교해야 하는 상황이 있기도 합니다. 이 문제처럼 그 조합을 찾는 과정이 바로 보이면 좋지만, 그렇지 않다면 헷갈리지 않게 네 가지 순서쌍을 확실히 표기하고 그 때 어떤 결과가 나타나는지를 구분하여 적어보면서, 문제의 조건과 논리적으로 모순이 되는 케이스를 제외하도록 합시다.


2021학년도 9평 물리학1 19번 문항
5. 자기장 파트 (난이도: 7/10)
○ 대표적인 준킬러 출제 내용: 패러데이의 법칙 응용
2022 수능에서는 물체의 자성, 패러데이의 법칙 응용, 직선 전류에 의한 자기장 응용 관련 문제가 각각 1개씩 출제되었습니다. 물체의 자성의 경우에는 강자성체, 상자성체, 반자성체의 특성에 대해 암기하고 있으면 쉽게 풀이할 수 있으므로, 나머지 두 문제를 다뤄 보겠습니다.
먼저 2022 수능의 12번 문제인데, 앞의 역학 파트 및 전기장 파트와도 연계되는 전형적인 패러데이의 법칙 응용 문제입니다. 여기서 '솔레노이드 관점에서 동일한 상황'이라고 표현한 것은, 주어진 문제에서 솔레노이드의 왼쪽을 L, 오른쪽을 R, 자석의 왼쪽을 S, 오른쪽을 N이라고 했을 때 L과 N의 근접은 R과 S의 근접과 동일한 효과를 일으키기 때문입니다. 조금 더 자세히 설명하면, 패러데이 법칙의 부호에 의해 솔레노이드와 자석이 가까워지면 솔레노이드가 자석과 같은 방향의 자석 역할을 하도록 전류가 흐르고, 멀어지는 경우에는 반대의 상황이 벌어지게 됩니다. 이렇게 솔레노이드와 자석 사이의 자기력은 자석의 속력을 감소시키는 방향으로 작용하기 때문에, 자석의 역학적 에너지가 감소하게 되는 거죠.


2022학년도 수능 물리학1 12번 문항
○ 대표적인 킬러 출제 내용: 직선 전류에 의한 자기장 응용 (퍼즐)
다음으로는 2022 수능의 18번 문제입니다. 기존에 출제되었던 비슷한 유형의 문제에 비해 퍼즐 풀이의 난이도가 까다로운 편이었습니다. 그렇기 때문에 풀이도 다소 복잡하게 보이는데, (i)-(ii)-(iii)-결론(빨간 상자) 순으로 이해하시면 됩니다. 이 문제에서는 A의 전류의 방향과 세기가 모두 주어져 있고, C의 전류의 세기와 P에서 A의 전류에 의한 자기장의 세기가 주어져 있네요. 그리고 P와 Q에서의 A, B, C의 전류에 의한 자기장의 세기가 표로 주어져 있고요. 이를 활용해 결국 C의 전류의 방향, B의 전류의 방향과 세기를 구하는 것이 문제에서 요구하는 바라고 할 수 있습니다.
(i)와 같은 방식으로 방향에 대한 부호를 임의로 설정하고, 문제의 조건에 맞게 거리와 전류의 세기에 따른 자기장의 세기를 식으로 표현하는 것이 첫번째 단계입니다.
이때, 세기 정보가 주어진 C의 전류의 방향을 각각 +y방향과 -y방향이라고 가정하면 P와 Q에서의 자기장의 세기가 어떻게 되는지 케이스를 나누어 살펴보는 게 (ii)의 단계가 되겠네요. 마지막으로 (iii)의 단계처럼 B의 전류의 방향을 각각 가정하여 표와 같은 결과를 얻을 수 있는 케이스를 찾으면 됩니다. 제가 풀이한 것처럼 4가지 케이스를 다 적어서 x에 관한 연립방정식을 풀이해 모순의 여부를 따져도 되지만, 이는 시간이 상당히 오래 걸리므로 숫자에 대한 감각(직관)을 활용하여 모순이 되는 케이스를 빠르게 제외하고 빨간 상자의 결론을 바로 얻는 것이 좋습니다. 실제로 저는 수능 시험장에서 (i), (ii)의 단계 이후, 머릿속으로 각각의 케이스 중 모순이 될 것 같은 케이스를 거르고 유일하게 가능할 것으로 예상되는 빨간 상자의 결론을 꽤 빠르게 얻었습니다.


2022학년도 수능 물리학1 18번 문항
6. 파동 파트 (난이도: 5/10)
○ 대표적인 준킬러 출제 내용: 서로 다른 매질의 경계에서 일어나는 굴절과 전반사의 이해 및 응용
2022 수능에서는 파동의 특성, 전자기파의 종류와 활용, 파동의 간섭의 활용, 굴절 및 전반사 관련 문제가 각각 1개씩 출제되었습니다. 전반사를 제외한 나머지 3문제의 경우는 개념의 정의와 활용 사례 등을 잘 기억하고 있으면 풀 수 있는 문제이니 따로 언급하지 않겠습니다. 그럼 2022 수능의 굴절 및 전반사 관련 문제인 11번을 풀어보겠습니다!
대략 다음과 같이 풀이할 수 있는데, 결국 굴절률과 파장 사이의 관계, 굴절률의 차이에 따른 입사각과 굴절각의 변화에 대한 이해가 요구되었던 것 같네요. 이를 통해 알 수 있는 파동 파트에서 기억해야 할 핵심 관계로는, 어떤 매질에서의 굴절률이 해당 매질에서 파동의 파장에 반비례한다는 것과 스넬 법칙에서 매질 간의 경계면을 기준으로 두 매질의 굴절률의 대소 관계와 입사각과 굴절각의 대소 관계가 반대라는 점 정도가 있습니다.

2022학년도 수능 물리학1 11번 문항
7. 빛과 물질의 이중성 파트 (난이도: 2/10)
○ 대표적인 준킬러(?) 출제 내용: 광전 효과 관련 실험의 해석, 빛 또는 전자선의 간섭 실험의 해석
2022 수능에서는 빛의 간섭과 광전 효과를 모두 확인할 수 있는 실험에 대한 해석 관련 문제가 출제되었습니다. 이 파트의 경우에는 이중성과 관련된 몇 가지 주요 실험의 결과에 대한 해석, 전하 결합 소자와 전자현미경의 원리, 물질파의 파장 정도만 알고 있으면 대부분의 문제를 어렵지 않게 풀이할 수 있습니다. 개인적으로 물리1에서 수능 문제 기준으로 가장 쉬운 파트라고 생각합니다. 특별한 풀이가 요구되지 않는 파트인 만큼 따로 문제 풀이는 하지 않겠습니다.
뭔가 막상 다 쓰고 보니, 2022 수능 비역학 해설에 가깝네요... 글로 작성한 내용에 단원별로 자주 출제되는 준킬러/킬러 유형과 해당 유형 문제의 접근법 정도는 포함된 것 같으니, 올해 물리1을 공부하시는 분들께 조금이나마 도움이 됐기를 바라며 글 마무리하겠습니다!
(다음 글은 기분에 따라 물1 역학 준킬러/킬러 접근법 or 화2 문풀법이 될 것 같아요ㅎㅎ)
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
역시 볶음밥에는 계란후라이가 있어야지
-
진학사 안정 2
200명 넘게 뽑는 대형관데 이정도면 무조건 붙을 수 있을까요?? 소신 2개 지르기...
-
어차피 홍대건축 못갈거 과기대 전기정보 6 국민대 전자 6 숭실대 전자정보 6 이렇게 박아버렸는데
-
그럴 생각임
-
친구랑 같이 쓸려했는데 기기 등록 3번인가 바꾸면 정지먹인다고 뜨네요 이제...
-
ㅅㅂ말도안돼
-
같은 학교 기준 어디가 취업 면에서 더 유리할까요..?
-
한 10개정도로 추림 ㅇㅇ
-
서울대 ㅇㄷ 쓸까요? 12
1. 첨단융합학부 - 54명 모집, 실지원자 기준 39등, 메디컬 걸려있는 사람 좀...
-
거 잠이나 자쇼
-
경인교대 6칸 최초합이고 홍대 역사교육과 5칸 추합 (10등 언저리) 입니다 반수는...
-
가군이 33명 모집과 1칸 (126/169) 나군은 13명 소수과 6칸 (중간...
-
진학사 6칸추합권인데 이정도면 붙는다고 생각해도 되나요?? 불안불안하네요 이거는 꼭 붙어야하는데..
-
중대 융공 2
융공 취업에 좋은 편인가요? 서울대 연세대 고려대 한양대 중앙대 현우진
-
아주좋아요
-
9kg 빠짐 / 9kg 더 빼야함 하루 3만보씩 걷는중 칼로리 제한도 하는중
-
인천에 살아서 통학은 1시간 정도 차이납니다. 대깨컴이면 숭실대가 더 좋은 선택일까요?
-
대부분 하위권인가요? 상위권인가요? ㅠㅠ 작년 경쟁률만큼 표본이 없는데 뭘 보고...
-
정확하게 써야 되나요?? 잘 기억이 안 나는데...
-
소수과 5칸추합러의 입시...
-
뭐가 더 어려울가요
-
사탐과탐 ㅈㅂ 1
외우는거 잘 못하고 쌉이과형 머리면 사탐보다 과탐이 유리할수가 았음??
-
ㅅㅂ 홍자전 못가는거에요?
-
진학사 업뎃 0
언제하나용
-
전 이번년도 7월에 전역하는 군인이고, 현재 패스는 입대때부터 이투스 월구독...
-
22개정 수능에서는 절대 볼 수 없는 확통 자작문제 바로 22개정교육과정 '확률과...
-
수특 표지설 1
26수능 쓰나미수능
-
고대썼어요 0
반드시 가야겠지?
-
뀨뀨 17
뀨우
-
얼른 원서 써야 한다고
-
얘가 예비 1번 받음
-
작년에 인설약 높았던 건 낮은 영어 1 비율 + 추합시즌에 증원 얘기가 나오며...
-
ㅈㄴ설레네 방학한 고3은 막을 수 없다
-
그마아안.....
-
저녁 먹으려는데 0
친구가 없어서 슬픈걸요.. 그냥 공부나 해야것다
-
하,,씨,, 아침에 미라클모닝하는 방법없나요,,,ㅠ 0
아침을 일찍 시작해야되는데, 그래서 막 화장실 사진 찍어야(각도랑 딱맞게) 알람...
-
고3이고 인강 들어본적 없어서 뭐가뭔지 잘모르겠네요 모고 232 나오고 사탐은...
-
모두를 위해 추천좀
-
표본도 더 안들어오고
-
어디가 낫나요?? 인식포함해서요
-
처음이라 ㅈㄴ떨리고 그냥 ㅈㄴ불안해요 저 숫자가 뭐라고 진짜 이거아니면 안되서...
-
입학처 들어갔는데 어디로 가야하나요? 지원 후에만 볼 수 있나요?
-
ㅜㅜㅜㅜㅜㅜ ㄹㅇ
-
어디쓰실건가요
-
srt 미친거 2
사람들이 왜이렇게 빨라
-
지거국 사탐런 1
국수영 잘 안돼있다는 가정하에도 지거국 목표로 사탐런 맞다고 보나요??? 고ㅏ탐...
-
나군만 내면끝 근데 아직 못정했어요
-
경제 응통 복수전공이 필수라면 학점을 안챙겨도 되는지, 아니면 다른 단과대생들처럼...


















































pv=nrt 열역학에서 개꿀
ㄹㅇㄹㅇ
매국노 메타에 귀한 물리 칼럼 감사해요 ㅎ..
좋은 칼럼 감사해요 팔로우해놓은 보람이 있네요
후배로 들어갈게요. 밥약해주세요.. 응애
이 칼럼은 다시 한번 재업하시는 것도 좋을것 같아요. 다른 메ㅐ타에 묻혀서 많은 분들이 못 본 거 같네요…ㅜㅜ
헉 조언 감사합니다... 이번 꺼는 좀 늦은 것 같아서 다음 글은 다른 분들이 많이 볼 수 있도록 해볼게요!!
혹시 역학 글은 언제 올라오나요?
잘읽었습니당!
원래 이번주에 작성하려고 했는데 생각보다 일정이 바빠서요ㅜㅜ 다음주 안에 작성하는 게 목표이긴 합니다!
헉 알겟숩니당 진짜 글 잘읽었어요! 감사합니다~