"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

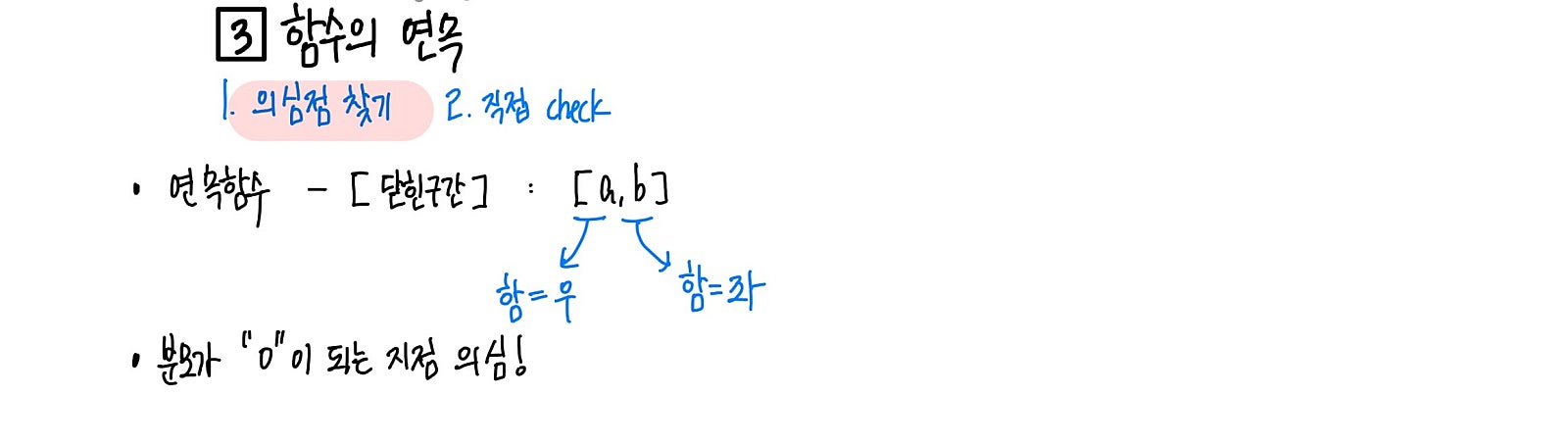
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
ㅇㅇ;
-
철인왕후고 사불이고 다리미고 맨날 어벙벙한 캐릭터로 나오네
-
학교 다니다가 전공이 적성에 안맞아 수능 재도전해보려 하는데 23 수능 97 90...
-
이번에 학사+대치 재종 생각하려다가 기숙 오픈한다 해서 고민중인 지방...
-
이명학 알고리즘 안 듣고 리로직 바로 들어가도 될까요? 1
최근에 대성 셀렉션인가 작년거 풀고 93점 나왔습니다 근데 빈칸만 2개가 나가서ㅠ...
-
복귀 0
Grandma 댁 가는중
-
인설약이 미쳤다고 하는데 그 이유가 대충 이래요 기존에는 지방의 같이쓰면 다 갔는데...
-
생2 좋은 과목 아님? 14
ㅇㅇ;
-
케바케겠지만 결국 공부할 '의지'는 자신에게 달려있는듯 약이 좋지만 만병통치제가...
-
여기 다녀오셈 남자BL학원 컨셉 카페임 공식 유튜브도 있음 가격도 무난하고 ㄱㅊ음...
-
솔직히 뉴진스 0
성공한 피프티 아니냐(여론만)
-
다음 닉 후보 13
블레임 이상한 Valuable
-
그냥 밤샐까요 1
어차피 내일 친척집 가야하는데 그때 하루종일 자고
-
문항 번호문항 배점DeepSeek 답변정답 (짝수형)오답 여부DeepSeek 풀이...
-
새터나 오티 술자리 이런거 한번도 안가보고 이제야 1학년 되는데 가도 되겠죠?...
-
10개 살거라서 추천 좀 해주쇼
-
학원교재 어려운거 쓰긴 하는데 혹시 실전개념이 너무 어려울까봐 걱정댑니다
-
윤석열 화이팅
-
파릇파릇한 새내기들과 낭만적인 대학라이프라니...
-
먹고 싶다
-
240628추억이다
-
밥부터 먹을까.
-
저도 요즘 4
수험생때에 준하는 분량의 문제들을 푸는 중
-
ㅈㄴ깊음
-
캬ㅑㅑ
-
얼굴이 가로로 넓다
-
아니 22
진짜 찐찐 네임드들에 비하면 미약한게 맞잖아 그 사람들만한 네임드가 되고 싶다거
-
치킨 맛있당 17
히히
-
열심히 썼는데 https://orbi.kr/00071620666
-
하..“여자”니까 사다준다 크하하하 이러니까 여자들이 뻑이가지
-
시간 지날수록 서울대 바로 밑으로 수렴할거라고 봄 ㅋㅋ 연약 22,23때도...
-
그아아아악
-
한가지만 우직하게 끝내는 사람이 되는게 힘들어.......
-
한 6개월 뒤면 14
나도 거대한 오르비 네임드가 될 수 잇을 거야
-
건국대는 사회환경공학부(토목) 동국대는 전기전자공학부입니다 둘다 정시로 넣었고...
-
예전에 만든것 1
-
금테가 빠를까 5
탈릅이 빠를까
-
현재 군수중이고 현역,재수 마치고 바로 입대하고 1년 쉰다음 다시 시작하는중....
-
특정인물이 인증하면 5초만에 블라먹는건 개꿀잼이었ㅇ.ㅁ
-
만두 만들기 28
맛있어요
-
후 방청소 완료 6
사진 찍어서 보여드리고 싶음 ㅋㅋ
-
막내임 11
08 옯창은 없음 07 옯창은 으으ㅡㅡㅁ.. 더 잇나?
-
현역때 93 100 2 95 99 였는데 가군쓸때 인설약 4칸이어서 고대로 쫄튀함
-
다들 가는구나 5
마이 해따 아이가
-
요즘애들수준 15
왤케 떨어짐?불행하게 피를 공유하고 태어난 암컷고릴라(중1)랑 1달?만에 대화하는데...
-
ㄱㅁ 9
4문제 중 4틀 ㄹㅈㄷㄱㅁ





















































